Differential Privacy and Publicly Known Constraints

Some papers have argued about a weakness in the definition of differential privacy; namely that it does not provide privacy when the dataset has correlated rows or when some public constraints about the dataset are known. Differential privacy is a mathematical notion of privacy for statistical analysis of sensitive datasets, i.e., datasets containing private data of individuals.

One of the claimed benefits of differential privacy over other alternative definitions, e.g., k-anonymity, data de-identification, is that the privacy guarantee holds even under arbitrary background knowledge of an adversary. The aforementioned weaknesses posit that this property of differential privacy is in fact not true in cases where the dataset has correlated rows or when some public constraints about the dataset are known. For instance, when exact query answers had already been released.

I will set aside the issue of correlated data, as others have already critiqued it. Indeed, finding statistical correlations is the goal of data analysis in the first place. The focus of this blogpost is instead on releasing differentially private answers when some constraints about the input dataset are already publicly known. This example is rather intriguing, and seems like highlighting a weakness in the definition of differential privacy. In essence, this could be considered an extreme form of correlated data. I will reproduce the example first, which is detailed here and here.

Publicly Known Constraints

Suppose a company hires employees at exactly 'm' different salary levels: 1, 2, ..., m. At some point in time, the company decides to release the number of employees under each salary level, which we denote as n₁, n₂, ..., n_m. The company wishes to do this in a privacy-preserving way, so that no one can tell the salary level of Alice, one of the employees of the company. We assume that Alice is at salary level 1. Let us further assume that there are 9 other employees with the same salary level as Alice. Thus, n₁ = 10. A standard way of releasing these counts via differential privacy is by adding Laplace noise of scale 1/eps to each of the counts n₁, n₂, ..., n_m, and then releasing the perturbed counts. Here "eps" stands for epsilon, the privacy budget.

Now, assume that the company had previously publicly released some constraints about this dataset (back when the company was less privacy conscious). More specifically, the company previously released the information:

The number of people at salary level 2 are 10 more than the number of people at salary level 1. That is: n₂ = n₁ + 10.

Not only this, but the company also released similar information about other salary levels:

n₃ = n₁ + a₃, n₄ = n₁ + a₄, ..., n_m = n₁ + a_m.

Here a₃, a₄, ..., a_m are positive integers, and we let a₂ = 10. With these constraints, we can write:

n₁ = n₂ - a₂, n₁ = n₃ - a₃, n₁ = n₄ - a₄, ..., n₁ = n_m - a_m.

These are a total of m - 1 constraints. Note that we still do not know what the n_i's are; there are m unknowns and m - 1 linear equations. However, once the noisy counts are released, we can replace n_i with its noisy version in the RHS of each of the constraints. Then, together with the noisy version of n₁, this gives us m estimates of n₁. We can average these m estimates, and then round the average to the nearest integer to get the true count n₁ with high probability (as a function of m). An attacker who knows all other employees' salary levels excluding Alice, can now know for sure that Alice has salary level 1. The success of this attack is shown below as a function of the number of attribute values (salary levels) m. The light blue band shows when the averaged out value is the true value of n₁.

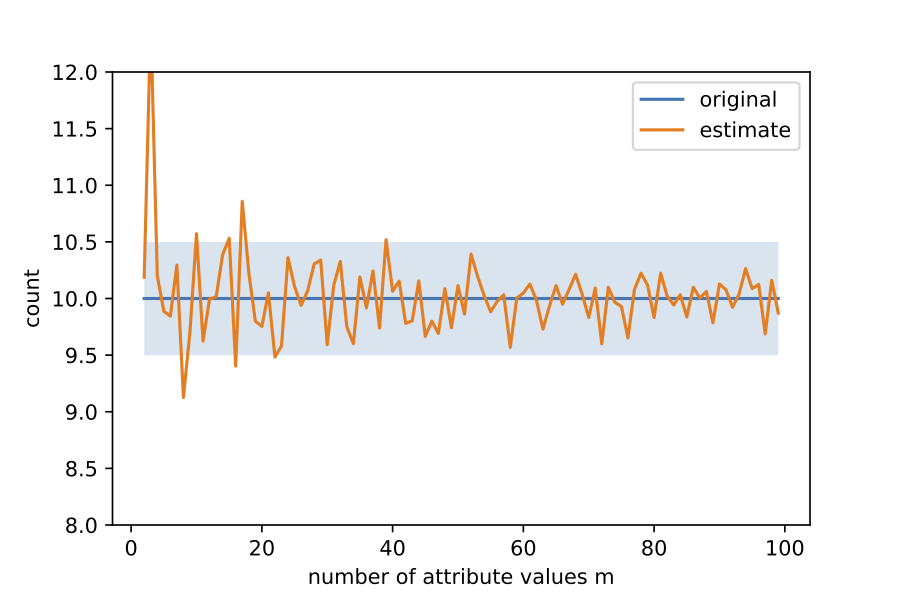
The example seems to imply that differential privacy's guarantee of privacy against arbitrary background knowledge is overstated.

The Catch

There is, however, some misinterpretation. The differential privacy guarantee is more accurately stated as: the output of a differentially private computation will not harm you more if your data were to be included even against arbitrary background knowledge. What this means is that what can be inferred with Alice's data can also be inferred without Alice's data. I would like to stress that these guarantees are stated in an informal way. Slightly different way of saying it (but again informally) is that the two worlds, one in which Alice's data is used in the differentially private computation and one without Alice's data are not easily distinguishable. In the example above, if we take Alice out of the count, i.e., n₁ is now 9 instead of 10, then the noisy version of n₁ is also different, i.e., it is now 9 + Lap(1/eps). However, if we release this count instead of the noisy count with Alice, it is still possible to solve the above constraints to find out the original value of n₁. In fact, even if we do not release n₁ at all, it is still possible to find the original value of n₁. This is illustrated in the figure below.

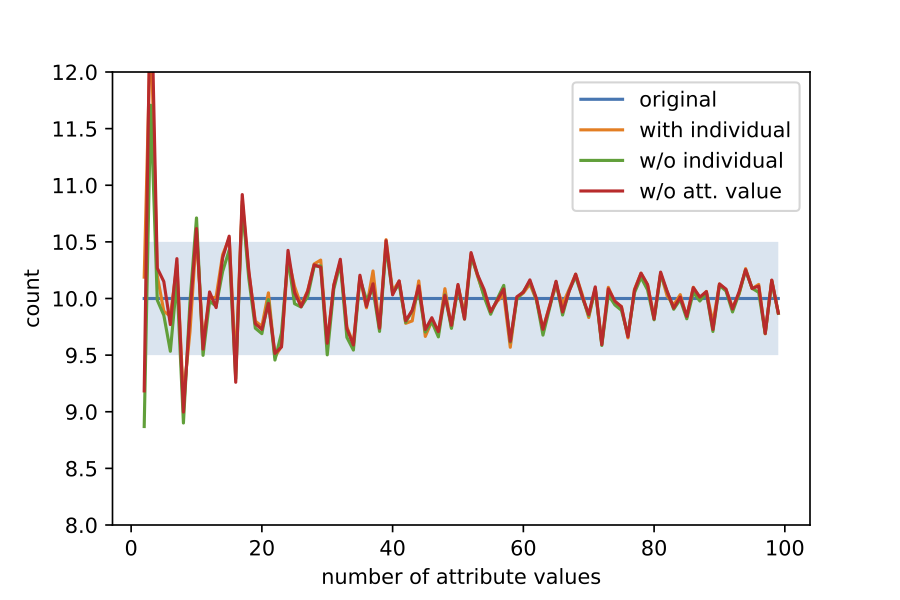
So What's Happening?

The main issue here is that Alice's information is tied to other individuals' information via the previous non-private data release. Thus, even if the dataset without Alice's data was used in the differentially private computation, the noisy release still tells the adversary about Alice. We can think of an even simpler example. Suppose, due to some weird equity policy, the company ensures that whenever a new person is hired at a certain salary level, the company needs to hire m - 1 other individuals at the m - 1 other salary levels. Thus, now we have the constraints n_i = n₁ for all i in {1, ..., m}. The data analyst, unaware of these constraints, releases n_i + Lap(1/eps) for each i. Once again the output can be averaged out to find the true count, if these constraints are known to the attacker.

Another way of interpreting differential privacy's guarantee is that the attacker needs to guess which of the two datasets is the input dataset given a differentially private output: one with n individuals (with Alice included) and the one with n - 1 individuals (without Alice). We can see that the adversary, even after finding the exact values of n_i's by averaging, cannot tell whether the differentially private data release was done with Alice's data or without. The problem is that the constraints themselves are leaking way too much information, meaning that Alice is merely a sitting duck. Her data is tied to the data of m - 1 other individuals (those who need to be hired once Alice was hired; equity policy). Her secret is no longer hers to keep.

Further Absurdities

First note that, if the company already knows that the constraints are public information, it can simply release one of the m counts using differential privacy, and then release the other m - 1 through the constraints. The blowfish privacy framework shows how to incorporate these constraints to release data in a privacy preserving way in a similar manner. However, this requires knowing what information is available to the adversary or what has been previously publicly released. One of the advantages of differential privacy is not needing to be concerned about background or public information. Differential privacy's privacy guarantee is tied to an individual. If Alice's data is linked to every other individual's data in the dataset (an extreme case of the m constraints), then there is an issue with the privacy expectation. The goal is to be able to infer database wide trends. Unfortunately, in this case database wide trends have Alice written all over them.

Lastly, another interpretation of differential privacy is that even if the attacker knows everything about the n - 1 individuals, he/she will not be able to infer information about the nth individual (assume Alice) via a differentially private release. However, if the attacker knows everything about the n - 1 individuals, and the publicly known constraints discussed above, then the attacker already knows all he/she needs to know. That is, the attacker can find n₁ from any of the m - 1 constraints, even without any differentially private release. Thus, differential privacy is causing no extra harm. For this interpretation to make sense, we might as well assume that the constraints themselves are constructed without Alice's data, i.e., the constraints are now n₁ = n_i - a₂ - 1, for all i in {2, ..., m}. Now, the attacker cannot distinguish between the two cases!